Digital frequency
Digital frequency is the analogue for discrete signals as frequency is to continuous signals. Since a discrete signal is a sequence (merely a series of symbols; typically, numbers) it contains no direct information as to determine the frequency of the corresponding continuous signal.
Just like in frequency, a digital frequency can have values in degrees or radians. However, it is common to represent a digital frequency that has been normalized to either the Nyquist frequency or the sampling frequency. It is therefore very important to specify the frequency range.
The following frequency ranges assume a signal has been properly sampled by satisfying the Nyquist-Shannon sampling theorem.
Contents |
Standard ranges
The values of a valid signal is in the range of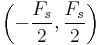 
hertz.
Likewise for radians, values of digital frequency are in the range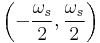 
radians.
Normalized ranges
The normalized hertz range is the hertz range divided by the sampling frequency. A valid signal is on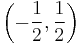 
cycles per sample.
Instead, the normalizing frequency could be the nyquist frequency, which puts a valid signal on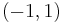 
cycles per sample.
For radians, normalized frequencies are in the range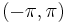 
, equivalent to half a cycle per sample.
Clearly a frequency of just "0.1" is insufficient to describe the true frequency of the discrete signal. To remove the ambiguity, it is necessary to specify the range and what normalization frequency was used (if applicable).